-
순조부 2 - 순열(Permutation)알고리즘/알고리즘 이론 2022. 10. 15. 12:39
순열은 서로 다른 n개 중 r개를 택하여 한 줄로 나열한 것이다.
순열을 코드로 표현하는 방법은 재귀, 비트마스킹, 넥퍼(Next Permutation) 3가지 방법으로 나타낼 수 있다.
재귀
- N개의 숫자를 배열에 저장
- 배열에서 각 위치의 숫자를 뽑았을 때, 뽑지 않았을 때의 순열을 생성
- 순열의 크기가 R개가 됐을 때 순열 완성
public class Permutation { // N개 중 R개의 순열 뽑기 static int N, R; // arr - 입력받을 배열 // temp - 순열을 저장할 배열 static int[] arr, temp; // 순열을 만들기 위해 arr의 요소가 선택됐는지 안됐는지 판단하는 배열 static boolean[] isSelected; public static void main(String[] args) throws IOException { BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); StringTokenizer st = new StringTokenizer(br.readLine()); N = Integer.parseInt(st.nextToken()); R = Integer.parseInt(st.nextToken()); arr = new int[N]; temp = new int[R]; isSelected = new boolean[N]; st = new StringTokenizer(br.readLine()); for (int i = 0; i < N; i++) { arr[i] = Integer.parseInt(st.nextToken()); } perm(0); } // 재귀로 순열 만들기 // arr의 요소를 하나씩 탐색하면서 temp에 순서대로 넣어본다. // 이미 선택된 요소는 선택하지 않는다. private static void perm(int cnt) { // 기저조건 // 순열의 크기가 찾고자하는 R의 크기가 되었을 때 재귀를 종료 if(cnt == R) { System.out.println(Arrays.toString(temp)); return; } for (int i = 0; i < N; i++) { // 이미 선택된 숫자일 경우 건너뛴다 if(isSelected[i]) continue; // cnt의 위치에 순서대로 arr의 값을 넣는다. temp[cnt] = arr[i]; // 선택된 숫자를 표시하고 재귀를 태운다. isSelected[i] = true; perm(cnt+1); // 해당 숫자의 사용을 해제한다. isSelected[i] = false; } } }입력
5 3 1 2 3 4 5출력
[1, 2, 3] [1, 2, 4] [1, 2, 5] ... [5, 4, 1] [5, 4, 2] [5, 4, 3]비트마스킹
비트마스킹도 기본적으론 재귀를 사용하지만 위에서 사용한 isSelected 대신 비트연산(Shift연산)을 활용하여 순열에 사용한 요소의 위치를 파악한다.
비트마스킹을 사용하면 isSelected와 같은 체크용 배열을 따로 관리하지 않아 공간복잡도면에서 좀 더 좋으며, 이진수를 이용해 연산을 하므로 연산 속도가 더 빠르다.
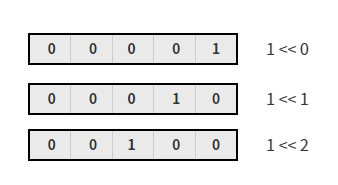
위 그림과 같이 1을 비트연산으로 이동하며 선택한 위치를 표시할 수 있다.
그럼 이걸 어떻게 사용하느냐?
and연산(&) 과 or연산(|) 을 사용하여 지금까지 순열에 사용된 요소들의 위치를 찾을 수 있다.

지금까지 사용한 값과 현재 탐색하는 요소의 index값을 and연산을 하여 0이 아니면
이전에 이미 선택된 요소인 것이다.
if((flag & 1<<i) != 0) continue;여기서 중요한건 연산 결과가 0이 아니다(≠ 0) 이다. 비트마스킹을 처음 배우면 ((flag & 1<<i) == 1) 이렇게 사용하는 경우가 있는데 위 그림을 보고 1이라고 생각하면 안된다. 이진수인걸 주의하면 위 그림의 결과는 4라는걸 알 수 있다.

이미 선택된 요소가 아닐 경우 새로 선택된 요소의 위치를 표시할 땐 or연산을 하여 표시한 후 그 값을 다음 재귀에 넘겨준다.
bitPerm(cnt+1, flag | 1<<i);isSelected를 사용하던 코드를 위 코드로 바꿔주면 BitMasking을 사용한 순열이다.
입력 및 결과는 재귀때랑 같다.
public class Permutaion_Bit { public static void main(String[] args) throws IOException { // 입력은 위 재귀코드와 똑같다. bitPerm(0, 0); } // 비트마스킹 순열 만들기 // arr의 요소를 하나씩 탐색하면서 temp에 순서대로 넣어본다. // 이미 선택된 요소는 선택하지 않는다. private static void bitPerm(int cnt, int flag) { // 기저조건 // 순열의 크기가 찾고자하는 R의 크기가 되었을 때 재귀를 종료 if(cnt == R) { System.out.println(Arrays.toString(temp)); return; } for (int i = 0; i < N; i++) { // 이미 선택된 숫자일 경우 건너뛴다 if((flag & 1<<i) != 0) continue; // cnt의 위치에 순서대로 arr의 값을 넣는다. temp[cnt] = arr[i]; // 선택된 숫자를 표시하고 재귀를 태운다. bitPerm(cnt+1, flag | 1<<i); } } }넥퍼(Next Permutation)
넥퍼는 정렬된 수를 사전 순으로 다음 순열을 생성하는 방식이다.
사전 순으로 생성하기 때문에 처음에 배열을 정렬하고 가장 작은 순열을 한 번 처리해야한다.
넥퍼의 알고리즘은 우선 배열을 오름차순으로 정렬한다. 그 다음 사전 순으로 다음으로 큰 순열을 생성하여 가장 큰 내림차순 순열이 될 때까지 반복한다.
- 뒤쪽부터 탐색하며 증가하는 구간 중 가장 큰 값(i)의 앞자리(i-1)을 찾는다.
- 뒤쪽부터 탐색하며 교환위치(i-1)보다 큰 값 위치(j)를 찾는다.
- 두 위치(i-1, j)를 교환한다.
- i부터 맨 뒤까지 오름차순으로 정렬한다.
아래 그림은 [1, 2, 3, 4] 를 예로들어 넥퍼를 진행하는 과정이다.

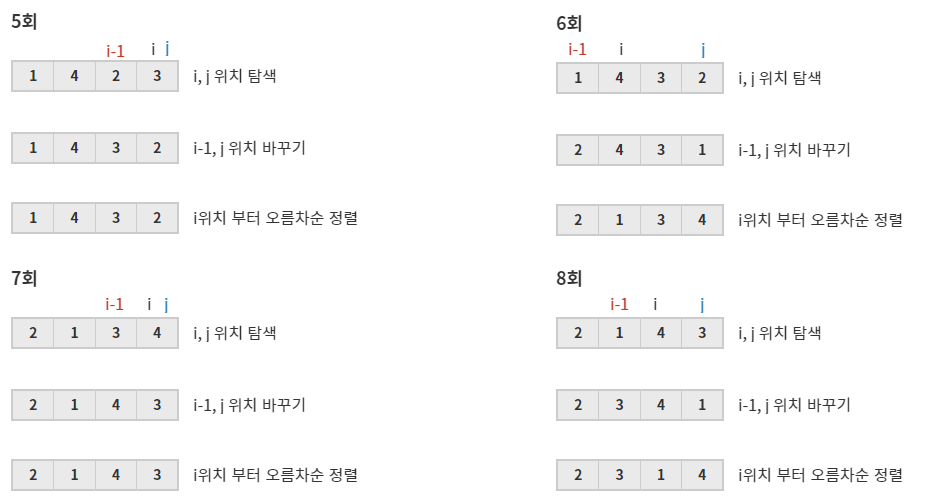

.
.
.

위와 같은 과정을 거쳐 가장 작은 순열부터 가장 큰 순열의 순서로 생성된다.
이제 과정을 알았으니 코드를 살펴보자, 코드는 생각보다 간단하므로 주석으로 설명을 대체한다.
public class NPTest { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int N = sc.nextInt(); int[] input = new int[N]; for (int i = 0; i < N; i++) { input[i] = sc.nextInt(); } // 오름차순 정렬 Arrays.sort(input); // 정렬된 순열을 먼저 출력 후 np를 태우기 위해 do-while 사용 do { System.out.println(Arrays.toString(input)); } while (np(input)); } public static boolean np(int[] numbers) { // 다음 순열 존재하면 true, 아니면 false int N = numbers.length; // 1. 뒤쪽부터 탐색하며 증가하는 구간 중 가장 큰 값(i)의 앞자리(i-1)을 찾는다. int i = N - 1; while (i > 0 && numbers[i - 1] >= numbers[i]) --i; // 다음 순열을 만들수 없는 이미 가장 큰 순열의 상태 if (i == 0) return false; // 2. 뒤쪽부터 탐색하며 교환위치(i-1)보다 큰 값 위치(j)를 찾는다. int j = N - 1; while (numbers[i - 1] >= numbers[j]) --j; // 3. 두 위치(i-1, j)를 교환한다. swap(numbers, i - 1, j); // 4. i부터 맨 뒤까지 오름차순으로 정렬한다. Arrays.sort(numbers, i, N); return true; } public static void swap(int[] numbers, int i, int j) { int tmp = numbers[i]; numbers[i] = numbers[j]; numbers[j] = tmp; } }'알고리즘 > 알고리즘 이론' 카테고리의 다른 글
순조부 1 - 순열, 조합, 부분 집합 (0) 2022.09.30